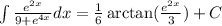The given integral expression is :
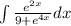
Apply u-substitution method :
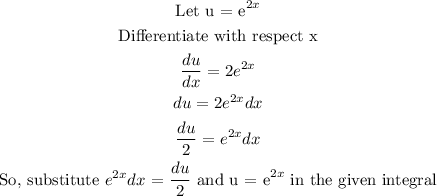
Thus the integral become :
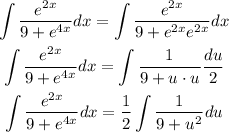
Apply the integral substitution : u = 3v
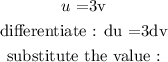
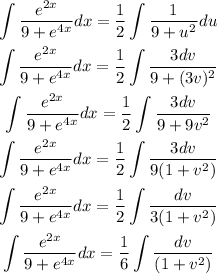
Apply the integral expression :
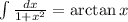
So, the expression will be :
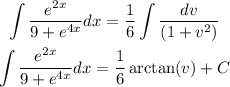
substitute the value of v = u/3
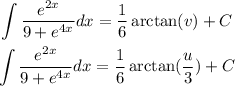
Now, substitute u = e^2x
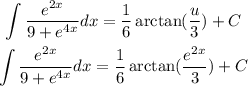
Answer :