SOLUTION
Since the scores are normally distributed, we will first obtain the Z score from Exam A, and then use it to find the score required from Exam B to meet that same Z score.
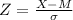
For Exam A, X(score)=45, M(mean)=35, S.D=5
Z will be:
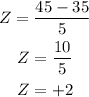
So to obtain, the score (X) for exam B, that will give us the same Z score.
For Exam B, X(score)=unknown, M(mean)=100, S.D= 25
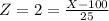

So Wyatt must score 150 in exam B in order to do equivalently well as he
did on exam A.