Question

A rectangular yard has a width to length ratio of 2:5. If the distance around the yard is 1400 feet, what are the dimensions of the yard?the yard is ______ ft wide and ______ ft long.

Answer 1

length = 500 ft

width= 200 ft

Step-by-step explanation:

Let us call w the width and L the length of the yard - then we know that

`(w)/(L)=(2)/(5)`

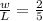
in other words, the length to width ratio is 2 : 5.

Moreover, we also know that the distance around the yard (its perimeter) is 1400 ft - meaning

`2(w+L)=1400`

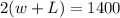
Hence, we have two equations and two unknowns.

Now for solve for w in the first equation to get

`w=(2)/(5)L`

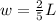
substituting this value of w in the second equation gives

`\begin{gathered} 2(w+L)=1400 \\ 2((2)/(5)L+L)=1400 \end{gathered}`

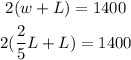
the left-hand side simplifies to give

`2((7)/(5)L)=1400`

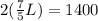
dividing both sides by 2 gives

`((7)/(5)L)=(1400)/(2)`
`\rightarrow((7)/(5)L)=700`

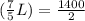
Multiplying both sides by 5/7 gives

`(5)/(7)\cdot((7)/(5)L)=700\cdot(5)/(7)`
`L=700\cdot(5)/(7)`
`L=(700\cdot5)/(7)`
`\boxed{L=500}`

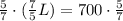
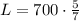
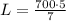
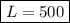
Hence, the length of the yard is 500 ft.

With the value of length in hand, we now find the width using

`w=(2)/(5)L`

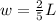
since L = 500, the above equation becomes

`w=(2)/(5)\cdot500`
`w=(2\cdot500)/(5)`
`\boxed{w=200}`

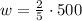
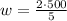
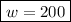
The width of the yard is 200 ft.

Hence, to summarize

The yard is 200 ft wide and 500 ft long.