Question

A line contains the points (-26,-37) and (-32, -61) what is the slope or the line?

Answer 1

Step 1. The two points we have are:

`\begin{gathered} (-26,-37) \\ \text{and} \\ (-32,-61) \end{gathered}`

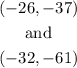
we will label these points as (x1,y1) and (x2,y2):

`\begin{gathered} x=-26 \\ y_1=-37_{} \\ x_2=-32 \\ y_2=-61 \end{gathered}`

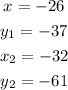
Step 2. Now that we have labeled the points, we can use the slope formula to find the slope ''m'' of the line:

`m=(y_2-y_1)/(x_2-x_1)`

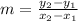
Substituting the known values:

`m=(-61-(-37))/(-32-(-26))`

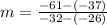
Step 3. Simplify the signs in the operations.

-(-37) is +37,

and -(-26) is +26:

`m=(-61+37)/(-32+26)`

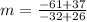
Step 4. Make the operations:

`m=(-24)/(-6)`

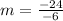
The result of this division is:

`m=4`

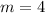
The slope of the line is 4.

Answer:

4