The average change of rate of a function in an interval is given by:
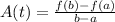
Where a and b are the left and right endpoints, respectively.
The endpoints are a = 3 and b = 3.1
Then, we do:
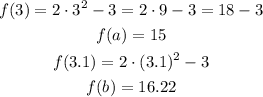
Then the average change of rate is:
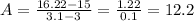
The average change of rate is 12.2
Now we need to find the instantaneous change of rate at the endpoints. This is the same as evaluate the derivative in the endpoints.
Then, the derivative of f(t) is:
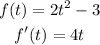
Then we evaluate f'(t) for t = 3 and t = 3.1:
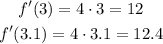
The rates of change are:
left endpoint = 12
right endpoint = 12.4