Question

For each sequence, determine weither it appears to be geometric or not.If it does, find the common ratio(a). 16, 4, 1, 1/4,...(b). 3, -6, 12, -24,...(c). 8, 10, 12, 14,...

Answer 1

Step-by-step explanation:

To find if the sequence is geometric we have to:

0. Divide each term by the previous term.

,

1. Compare the quotients. If they are the same, a common ratio exists and the sequence is geometric.

a. 16, 4, 1, 1/4...

First we divide each term by the previous term:

`\begin{gathered} (4)/(16)=(1)/(4) \\ (1)/(4)=(1)/(4) \\ ((1)/(4))/(1)=(1)/(4) \end{gathered}`

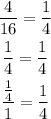
All these quotients are the same. This means that this sequence is geometric and its common ratio is 1/4

b. 3, -6, 12, -24...

Divide each term by the previous one:

`\begin{gathered} (-6)/(3)=-2 \\ (12)/(-6)=-2 \\ (-24)/(12)=-2 \end{gathered}`

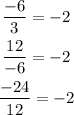
All these quotients are equal. Therefore this sequence is geometric and its common ratio is -2

c. 8, 10, 12, 14...

Divide

`\begin{gathered} (10)/(8)=(5)/(4) \\ (12)/(10)=(6)/(5) \\ (14)/(12)=(7)/(6) \end{gathered}`

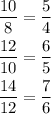
These quotients are all different. This is not a geometric sequence

Answers:

a. It is geometric. Common ratio = 1/4

b. It is geometric. Common ratio = -2

c. It is not geometric