To solve the quadratic equation, we must factorize the left side into two factors
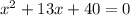
We have to look for two numbers their product = 40, and their sum = 13
Since 8 x 5 = 40 and 8 + 5 = 13, then the factors will be
(x + 5) and (x + 8)

Now we will equate each factor by 0
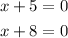
Let us solve them to find the values of x
x + 5 = 0
Subtract 5 from both sides
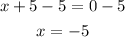
x + 8 = 0
Subtract 8 from both sides
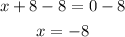
The solution of the equation is
x = -5 and x = -8
The answer is
x = -5 and x = -8