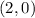Question

Here is a system of equations {y=-x+2{y=-2x+4Graph the system then write its solution

Answer 1

ANSWER and EXPLANATION

We want to graph the system of equations and solve them.

To graph a linear equation, we can use two points and then join them.

The two points to be used will be the x and y-intercepts.

To find the x-intercept by finding the value of x when y is 0.

To find the y-intercept by finding the value of y when x is 0.

For the first equation:

`y=-x+2`

The x-intercept is:

`\begin{gathered} 0=-x+2 \\ \Rightarrow x=2 \end{gathered}`

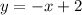
The x-intercept is (2, 0)

The y-intercept is:

`\begin{gathered} y=0+2 \\ y=2 \end{gathered}`

The y-intercept is (0, 2)

For the second equation:

`y=-2x+4`

The x-intercept is:

`\begin{gathered} 0=-2x+4 \\ 2x=4 \\ x=(4)/(2) \\ x=2 \end{gathered}`

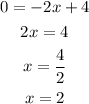
The x-intercept is (2, 0)

The y-intercept is:

`\begin{gathered} y=0+4 \\ y=4 \end{gathered}`

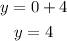
The y-intercept is (0, 4)

Let us plot the graph of the equations:

The red line represents y = -x + 2

The blue line represents y = -2x + 4

The solution to a system of equations is the point where the lines intersect one another.

Therefore, the solution to the system equations is:

`(2,0)`