In parallelograms, opposite sides are equal in length.
There are 2 pair of parallel sides.
In parallelogram ABCD, the congruent sides are:
• AB = CD
and
• AD = BC
Let's equate AB = CD and solve for x:

Now, let's equate AD = BC and solve for x:
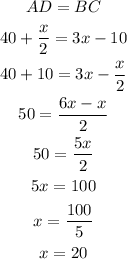
Thus, the x value is equal to 20.
Quadrilateral ABCD is a parallelogram.