Question

The parallelogram below is dilated by a scale factor of 1/2 about the point A(2,0) and then translated seven units to the right.  What is the location of R after the composition of transformations? F.(-2,3)G.(5,3)H.(0,0)J.(−3,3)

Answer 1

Given the vertices of the parallelogram:

P(-4, 3), Q(-8, 3), R(-6, 6), S(-2, 6)

Scale factor of dilation = ½

Center of dilation = A(2, 0)

To perform a dilation, all points are multiplied by the scale factor to find the new points of the dilated figure.

Given a center of dilation A(2, 0), let's ind the new points of point R:

Given: R(-6, 6)

Distance between R and center of dilation =

After a dilation of 1/2

`(-2,\text{ 3)}`

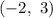
Translated 7 units to the right:

(x, y) ==> (x + 7, y)

(-4, 3) ==> (-2 + 7, 3) ==> (5, 3)

Therefore, the location of R after the compositipns of the transformation is:

(5, 3)