Answer:
6 pounds of strawberry
6 pounds of pineapples
Step-by-step explanation:
Let,
s = number of pounds of strawberry
p = number of pounds of pineapples
Now we are told that Malcolm is making 12 pounds of fruit salad with pineapple and strawberries. This means
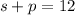
Furthermore, we are also told that Pineapples cost $7.50 per pound and strawberries cost $10.50 per pound. This means that the cost of the mixture will be
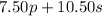
Therefore, the cost per pound of the mixture is
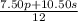
which we are told is $9 per pound. Therefore,
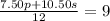
We can multiply both sides of the above equation by 12 and get:

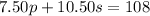
Hence, we have two equations and two unknowns:

To solve the above system for s and p, we first solve for p in the first equation.
Subtracting s from both sides of the first equation gives
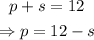
Substituting this value of p in the second equation gives

which we expand to get
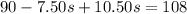
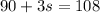
Subtracting 90 from both sides gives

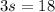
Finally, dividing both sides by 3 gives
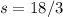
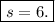
WIth the value of s in hand, we now find p.
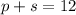
Putting s = 6 into the above equation gives
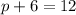
subtracting 6 from both sides gives
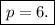
Hence, s = 6 and p = 6. This means, 6 pounds of strawberry and 6