To obtain the slope of a line given two points, use the formula below

In our case,
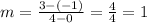
Then, in general, the slope-intercept form of the equation of a line is
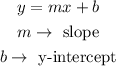
Thus, in our case,
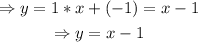
a) The equation of the line is y=x-1. To graph it, draw (4,3) and (0,-1) on the plane; then, cross them using a line, as shown below
b) Set y=0 in the equation we found in part a); then, solve for x, as shown below
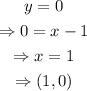
The x-intercept of the line is (1,0)