Given data:
* The mass of the bullet is 18.8 gm.
* The initial speed of the bullet is 399 m/s.
* The initial speed of the bullet is 0 m/s.
Solution:
The net momentum of the system before the collision of the bullet with the wooden block is,
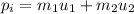
where m_1 is the mass of bullet, m_2 is the mass of wooden block, u_1 is the initial speed of the bullet, and u_2 is the initila speed of the wooden block,
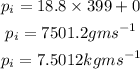
The final momentum of the system is,
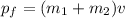
As bullet and wooden board behaves as a single body,
Substituting the known values,
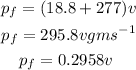
According to the law of conservation of momentum, the momentum of the system before and after remain same.
Thus,

Thus, the final velocity of the bullet is 25.36 meter per second.