Answer:
12 regular
15 large
10 extra large
Step-by-step explanation:
Variables:
s = number of coffees with regular size
l = number of coffees with large size
e = number of coffees with extra large size
Equations.
Equation for the quantity of coffees sold:
we add all of the quantities s, l and e:
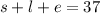
this is because the diner sold a total of 37 coffees. This will be equation 1.
Equation for the volume of coffee:
We need to multiply the volume that each side has with the number of coffees with that size:
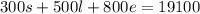
This is because the total volume of coffee sold was 19100mL. This will be equation 2.
Equation for the coffee sales:
We multiply the price of each coffee by the amount of coffes with that price:
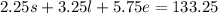
This is because the small cost $2.25, the large $3.25 and the extra large $5.75, and the total of coffee sales was $133.25. This will be equation 3.
Solve.
There are many ways to solve a 3 variable system of equations. I will multiply the first equation by -300 to add it to the second equation and eliminate s.
Multiply 1 by -300:
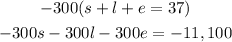
Now we add this to equation 2
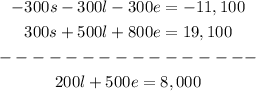
I will call this equation 4.
Next, we will use equation 2 and equation 3 to eliminate the same variable s, for this we multiply equation 2 by -2.25
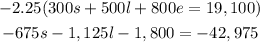
and equation 3 by 300:
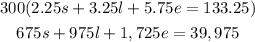
And we add this two equations to elimate s:
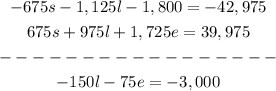
This will be equation 5.
Now we use equations 4 and 5 to find l and e. For that, we multiply equation 5 by 4/3:
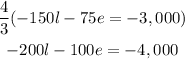
And add this to equation 4:
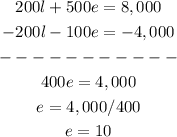
We have the value of e. Now we substitute this into equation 5, to solve for l:
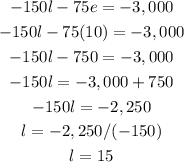
We have tha value of l, now we need to substitute e and l into equation 1 to find s:
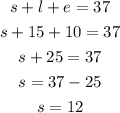
Answer:
12 regular
15 large
10 extra large