Question

Complete this sequence.-30,-22 ,-14, -6,2, [?]Enter the number that goes in the green box.

Answer 1

In the given sequence, we have an arithmetic sequence which is given by the following formula:

`a_n=a_1+(n-1)d`

Where an is the nth term of the sequence, a1 is the first term, n is the number of terms and d is the common difference.

We can find the common difference by applying the formula:

`d=a_n-a_(n-1)`

If we replace an=-22 and an-1=-30, we find:

`\begin{gathered} d=-22-(-30) \\ d=-22+30 \\ d=8 \end{gathered}`

The common difference is d=8.

The number that goes in the green box is the 6th term of the sequence. Then a1=-30, n=6, d=8. Replace these values into the formula and solve:

`\begin{gathered} a_6=-30+(6-1)\cdot8 \\ a_6=-30+(5)\cdot8 \\ a_6=-30+40 \\ a_6=10 \end{gathered}`

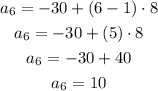
The answer is 10.