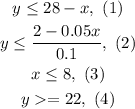Question

justin has x nickels and y dimes, having a maximum of 28 coins worth a minimum of $2 combined. at most 8 of the coins are nickels and no more than 22 of the coins are dimes. solve this system of inequalities qraphically and determine one possible solution.

Answer 1

We are given that x is the number of nickels and y the number of dimes. Since there must be at maximum 28 of them, we can express this mathematically like this:

`x+y\le28`

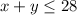
We are also told that they combine must be worth a minimum of $2, this means mathematically:

`0.05x+0.1y\ge2`

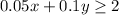
Now we are told that the number of nickels is less than 8 and the number of dimes is more than 22, this can be expressed mathematically as:

`\begin{gathered} x\le8 \\ y\ge22 \end{gathered}`

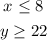
Therefore we have the following system of inequalities

`\begin{gathered} x+y\le28,\text{ (1)} \\ 0.05x+0.1y>=2,\text{ (2)} \\ x\le8,\text{ (3)} \\ y\ge22,\text{ (4)} \end{gathered}`

The graph this inequation is the following:

The possible solutions to the inequations are located where all the colors intercept.

For example, we can take the following point:

`(x,y)=(5,22)`

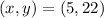
For inequality (1)

`\begin{gathered} x+y\le28 \\ 5+22\le28 \\ 27\le28 \end{gathered}`

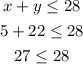
For inequality (2)

`\begin{gathered} 0.05x+0.1y\ge2 \\ 0.05(5)+0.1(22)\ge2 \\ 2.45\ge2 \end{gathered}`

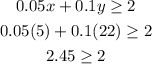
Since 5<8 and 22=22 this is a solution to the inequality.

The inequalities can be rewritten as:

`\begin{gathered} y\le28-x,\text{ (1)} \\ y\le(2-0.05x)/(0.1),\text{ (2)} \\ x\le8,\text{ (3)} \\ y>=22,\text{ (4)} \end{gathered}`