Question

determine the length of each side of rectangle abcd shown on the coordinate grit to identify congruent sides then find the area of the rectangle find the length of ABfind the length of BC

Answer 1

To fin the length of the sides of rectangle ABCD, we will be using the distance formula.

`d=√((x_1-x_2)^2+(y_1-y_2)^2)`

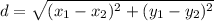
Let's first identify the coordinate of each point.

A (-4, 2)

B (-2, 4)

C (4, -2)

D (2, -4)

The coordinates will be used to substitute for the x's and th y's in the distance formula.

The length of AB is calculated as:

`\begin{gathered} AB=√([-4-(-2)]^2+(2-4)^2) \\ AB=√((-2)^2+(-2)^2) \\ AB=√(4+4) \\ AB=√(8) \\ AB=2√(2) \end{gathered}`

Meanwhile, BC's length is:

`\begin{gathered} BC=√((-2-4)^2+[4-(-2)]^2) \\ BC=√((-6)^2+6^2) \\ BC=√(36+36) \\ BC=√(72) \\ BC=6√(2) \end{gathered}`

We follow the same steps in calculating hte lengths of CD and AD:

`\begin{gathered} CD=√((4-2)^2+[-2-(-4)]^2) \\ CD=√(2^2+2^2) \\ CD=√(4+4) \\ CD=√(8) \\ CD=2√(2) \end{gathered}`
`\begin{gathered} AD=√((-4-2)^2+[2-(-4)]^2) \\ AD=√((-6)^2+6^2) \\ AD=√(36+36) \\ AD=√(72) \\ AD=6√(2) \end{gathered}`

The lengths of the sides of rectangle ABCD are:

AB = 2√2

BC = 6√2

CD = 2√2

AD = 6√2

The area of a recatangle is equal to the product of its length and width.

`\begin{gathered} Area=L* W \\ Area=(6√(2))(2√(2)) \\ Area=12(2) \\ Area=24units^2 \end{gathered}`

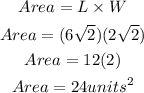
The area of rectangle ABCD is 24 square units.