We can solve this using a system of equations.
Let p be the price of 1 ounce of peanuts and c be the price of 1 ounce of cashews.
"...the first mixture has 15 oz of peanuts combined with 5 oz of cashews, and cost $6." gives us our first equation, that is:
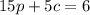
"...the second mixture has 5 oz of peanuts and 15 oz of cashews, and cost $8." gives us our second equation, that is:
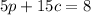
Thereby, the system would be:
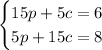
Let's mulitply the first equation by -3 and add both of them up:
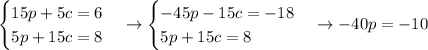
Solving for p,
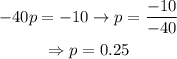
Let's plug in this value in equation 2 and solve for c, as following:
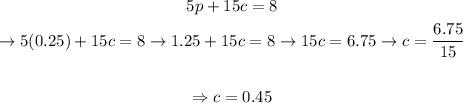
This way, we would have that
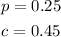
Meaning that an ounce of peanuts costs $0.25, and an ounce of cashews costs $0.45