Given the vertices of quadilateral WXYZ:
W(-1, 6), X(2, 8), Y(1, 0), Z(-2, -2)
A quadilateral is a figure that has four sides.
A parallellogram is a quadilateral with two pairs of parallel sides. The opposite sides of a parallelogram have equal lengths.
We have the figure of the parallelogram below:
Therefore, to prove this is a parallelogram, the slope of WX and YZ must be the same and the distance between WX and distance between YZ must be the same
To find the slope of line WX and the slope of line YZ, use the slope formula:
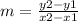
We have:
Slope of line WX
Take the points: (x1, y1) ==> W(-1, 6)
(x2, y2) ==> X(2, 8)
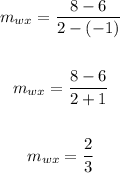
Slope of YZ:
Take the points: (x1, y1) ==> (1, 0)
(x2, y2) ==> (-2, -2)
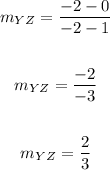
The slope of Lines WX and YZ are the same
To find the distance between WX and the distance between YZ use the distance formula:
![d=\sqrt[]{(x2-x1)^2+(y2-y1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/1h551ypq5weta3sw0dynfch7nxiwrgmnba.png)
• DIstance between WX:
Take the points: (x1, y1) ==> W(-1, 6)
(x2, y2) ==> X(2, 8)
![\begin{gathered} WX=\sqrt[]{(2-(-1))^2+(8-6)^2} \\ \\ WX=\sqrt[]{(2+1)^2+(8-6)^2} \\ \\ WX=\sqrt[]{3^2+2^2} \\ \\ WX=\sqrt[]{9+4} \\ \\ WX=\sqrt[]{13} \\ \\ WX=3.6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1dj8pr7e44tgsvny5ircz36ezzrubrecuy.png)
Distance between YZ:
Take the points: (x1, y1) ==> (1, 0)
(x2, y2) ==> (-2, -2)
![\begin{gathered} YZ=\sqrt[]{(-2-1)^2+(-2-0)^2} \\ \\ YZ=\sqrt[]{(-3)^2+(-2)^2} \\ \\ YZ=\sqrt[]{9+4} \\ \\ YZ=\sqrt[]{13} \\ \\ YZ=\text{ 3.6} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ou8bdlgyo7cmhqrje3vl83bo710f0n7i4r.png)
The distance between WX and the distance between YZ are the congruent.
Therefore, this quadilateral is a parallelogram.
Quadilateral WXYZ is a parallelogram by the opposite sides parallel and congruent theorem.
ANSWER:
Slope of WX = 3/2
Slope of YZ = 3/2
WX = √13
YZ = √13
Quadilateral WXYZ is a parallelogram by the opposite sides parallel and congruent theorem.