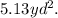Notice that the area of the shaded region is the area of the semicircle minus the area of the triangle.
To compute the area of the semicircle, we use the following formula:
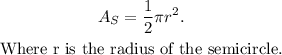
Substituting r=3yd and π=3.14 we get:
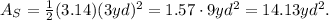
Now, notice that the base of the triangle is the diameter of the semicircle, and its height is the radius, using the formula for the area of a triangle we get that:
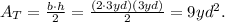
Finally, the area of the shaded region is:
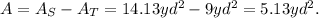
Answer: