Question

The sun of three numbers is 3. The first number minus the second plus the third is - 3. The first minus the third is 1 more than the second. Find the numbers.What is the first number?What is the second number?What is the third number?

Answer 1

Let x be the first number, y the second one, and z the third one, then we can set the following system of equations:

`\begin{gathered} x+y+z=3, \\ x-y+z=-3, \\ x-z=y+1\Rightarrow x-y-z=1. \end{gathered}`

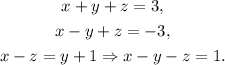
Adding the last equation to the first one we get:

`\begin{gathered} x+y+z+x-y-z=3+1, \\ 2x=4, \\ x=2. \end{gathered}`

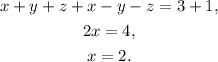
Now, adding the first two equations and substituting x=2 we get:

`\begin{gathered} 2+y+z+2-y+z=3-3, \\ 4+2z=0, \\ z=-(4)/(2), \\ z=-2. \end{gathered}`

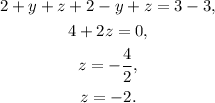
Finally, substituting x=, z=-2 in the first equation and solving for y we get:

`\begin{gathered} 2+y-2=3, \\ y=3. \end{gathered}`

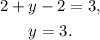
Answer: The first number is 2, the second one is 3 and the third one is -2.