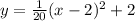Parabolas
We are given the graph of a parabola and from it, it's required to find its vertex, directrix, and focus.
There is no direct way to find those parameters directly from the plain graph, so we must find the equation first from the options given in the question.
First, we identify the parabola opens up, thus its directrix must be horizontal, and the focus is located above the vertex at a distance of p units (p is to be found later).
The general equation of a vertical parabola is:
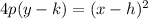
It's clear that the squared variable must be x. Thus, we can discard the first and third options.
A closer look at the graph shows its vertex is located at (2, 2). Substituting in the equation:
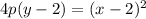
Solving for y:

This equation corresponds to the last equation:
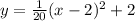
Where we can find the value of p = 20/4 = 5
The focus is located 5 units above the vertex, thus its coordinates are F(2, 7)
The directrix is located 5 units below the vertex, thus its equation is y = -3
Summarizing:
Vertex (2, 2)
Focus (2, 7)
Directrix y = -3
Equation: