We have to sketch the graph of y:
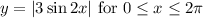
This is a transformed function.
We start by looking at sin(2x). This is the sine function but with a frequency that is twice the frequency of sin(x).
As sin(x) makes one cycle from 0 to 2π, then sin(2x) will make 2 cycles in the same interval of x.
Then, we multiply the amplitude by 3. This means that when sin(2x) is 1, its maximum value, our function will have an amplitude of 3.
Finally, we apply the absolute value function, where the negative values become positive: