We know that:
- a rocket is launched from the top of an 8-foot ladder.
- It’s initial velocity is 128 feet per second, and it is launched at an angle of 60* with respect to the ground
And we must write parametric equations that describe the motion of the rocket as a function of time
To write the parametric equations we need to know that the parametric general equations for a Projectile Motion are:
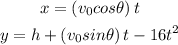
Where,
v0 represents the initial velocity
h represents the initial height
θ represents the angle respect to the ground
In our case,

Finally, replacing in the parametric equations:
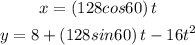
ANSWER:
![\begin{gathered} x=(128cos60\operatorname{\degree})t \\ y=8+(128s\imaginaryI n60\degree)t-16t^2 \end{gathered}]()