Question

Write a system of equations for each scenarios and solve.You need to buy two kinds of notebooks for your new class. A spiral costs $2.25 and a three-ring notebook costs $6. You need 7 notebooks. The cost of the notebooks totaled $27 before taxes. How many of each type were purchased?

Answer 1

Since there are two types of notebooks the sum of the number of each type should be equal to the total of notebooks bought, therefore:

`x+y=7`

x+y=7

Where "x" represents the number of spiral notebooks and "y" represents the number of three-ring notebooks.

If we multiply the number of each nobtebooks by their respective cost we should get the total value of the purchase, which is done below:

`2.25\cdot x+6\cdot y=27`

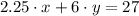
2.25x+6y=27

The system of equations is:

`\mleft\{\begin{aligned}x+y=7 \\ 2.25\cdot x+6\cdot y=27\end{aligned}\mright.`

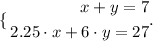
x+y=7

2.25x+6y=27

To solve this system of equations we need to eliminate one variable. To do that we will multiply the first equation by -2.25

-2.25x-2.25y=-15.75

2.25x+6y=27

Now we will sum both equations as shown below:

-2.25x+2.25x-2.25y+6y=-15.75+27

3.75y=11.25

y=11.25/3.75=3

The value of y is 3, if we use it on the first equation we can find the value of x. We have:

x+3=7

x=7-3=4

With this we've solved the system. The purchase was 4 spiral notebooks and 3 three-ring ones.