Question

Determine the number of solutions for the following system of linear equations. If there is only one solution, find the solution.No solution? Only one solution? Infinitely many solutions?

Answer 1

No solution

Step-by-step explanation:

Given the below system of linear equations;

`\begin{gathered} -5x+y+3z=2\ldots\ldots\ldots.\ldots\text{Equation 1} \\ -x+2y-z=2\ldots\ldots\ldots\ldots\ldots\text{Equation 2} \\ 6x-3y-2z=-1\ldots\ldots\ldots\ldots\text{.Equation 3} \end{gathered}`

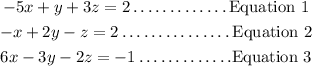
We'll follow the below steps to solve the given system of equations;

Step 1: Make y in Equation 1 the subject of formula by adding 5x to both sides and subtracting 3z from both sides as seen below;

`\begin{gathered} -5x+5x+y+3z-3z=2+5x-3x \\ y=2+5x-3z\ldots\ldots\ldots.....\ldots..\text{Equation 4} \end{gathered}`

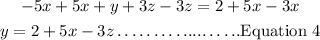
Step 2: Put Equation 4 into Equation 2, we'll have;

`\begin{gathered} -x+2(2+5x-3z)-z=2 \\ -x+4+10x-6z-z=2 \\ 9x-7z=-2\ldots\ldots\text{.}\mathrm{}\text{Equation 5} \end{gathered}`

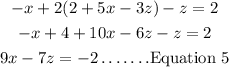
Step 3: Put Equation 4 into Equation 3;

`\begin{gathered} 6x-3(2+5x-3z)-2z=-1 \\ 6x-6-15x+9z-2z=-1 \\ -9x+7z=5\ldots\ldots\text{.}\mathrm{}\text{Equation 6} \\ \end{gathered}`

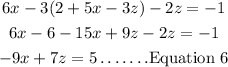
Step 4: Add Equation 5 and Equation 6;

`\begin{gathered} (9x-7z)+(-9x+7z)=-2+5_{} \\ 9x-7z-9x+7z=3 \\ 0=3 \end{gathered}`

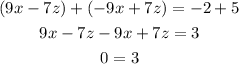
We can see that adding Equation 5 and 6 gave us 0 = 3 which is not a valid equation, therefore, we can say that the given system of equations has no solution.