Question

Help me I need somebody to show me how to do it.

Answer 1

We have a data set summarized as a stem-and-leaf plot

Recall that a stem and leaf diagram displays numerical data by separating each data point into a "leaf" (usually the last digit) and a "stem" (the leading digit(s))

In this case, we have 4 stems

In the first stem, we have 8 leaves that are to say 8 data

In the second stem, we have 16 data, in the third stem we have 5 data and in the last stem we have 3 data

First

n is the sum of all the data, n gives us the following

`\begin{gathered} n=8+16+5+3 \\ n=32 \end{gathered}`

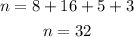
The answer is n=32 data set

Second

Now, the last class corresponds to the last stem, the minimum value of the last class is 80

8 is the stem, and the minimum leave is 0 for this reason the number is 80

Third

The modal class refers, in a table of grouped data, to the class or interval that has the highest frequency

In this case, is the 6 stem, and as frequency is 16

The frequency is the number of data to the associated group

Fourth

To find out how many numbers are greater than 60 we must count all data greater than 60

When we do this we know that the groups on stems 7 and 8 are inside the constraint and those on stem 5 are outside

Now we count the possible root 6 data with leaves that are greater than 0, when we do this we have 13 data

Then the data that is greater than 60 is:

`5+3+13=21`

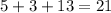
This answer is 21 data