Question

Select the correct answer.Which point lies on the circle represented by the equation (x+5)²+(y-912-827OA (0.8)OB. (13.9)OC. (5.1)OD. (3.17)

Answer 1

Given:

Equation of circle is:

`(x+5)^2+(y-9)^2=8^2`

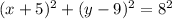
Find-:

Which point lies in the circle

`\begin{gathered} A.(0,8) \\ \\ B.(13,-9) \\ \\ C.(-5,1) \\ \\ D.(3,17) \end{gathered}`

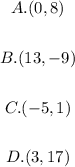
Explanation-:

If the points lie on a circle then it's true for the equation then,

(A)

Point is (0,8)

`(x,y)=(0,8)`

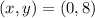
Check for the equation is:

`\begin{gathered} (x+5)^2+(y-9)^2=8^2 \\ \\ (0+5)^2+(8-9)^2=8^2 \\ \\ 25+1=64 \\ \\ 26\\e64 \end{gathered}`

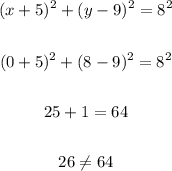
So it is a not a point in circle

(b)

Point is (13,-9)

`\begin{gathered} (x+5)^2+(y-9)^2=8^2 \\ \\ (13+5)^2+(-9-9)^2=8^2 \\ \\ 18^2+(-18)^2\\e8^2 \end{gathered}`

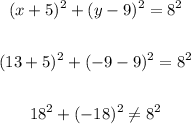
So it is a not a point in circle

(c)

Point (-5,1)

`\begin{gathered} (x+5)^2+(y-9)^2=8^2 \\ \\ (-5+5)^2+(1-9)^2=8^2 \\ \\ 0^2+(-8)^2=8^2 \\ \\ 64=64 \end{gathered}`

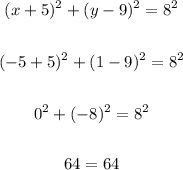
So, the point (-5,1) lies on circle.