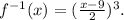12) To answer this question, we will set the equation y=f(x), solve for x, and then exchange x and y.
Setting y=f(x) we get:
![y=9+2\sqrt[3]{x}.](https://img.qammunity.org/2023/formulas/mathematics/college/57icxuk5qngz8qqa07botpag66ok6awz7u.png)
Subtracting 9 from the above equation we get:
![\begin{gathered} y-9=9+2\sqrt[3]{x}-9, \\ y-9=2\sqrt[3]{x}. \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fnaa8razajsqdg22qpd4uerl3h0igzux3e.png)
Dividing the above equation by 2 we get:
![\begin{gathered} (y-9)/(2)=\frac{2\sqrt[3]{x}}{2}, \\ (y-9)/(2)=\sqrt[3]{x}. \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/l2opjjnac3jnos3s9njl0i0kixxrrxnxdt.png)
Taking the above equation to the power of 3 we get:
![\begin{gathered} ((y-9)/(2))^3=(\sqrt[3]{x})^3, \\ ((y-9)/(2))^3=x. \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/iyc007afgdsrxa8tm10i3jdr6k1kp89bcw.png)
Exchanging x and y we get:
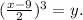
Therefore:
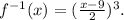
Answer: