We have the point A(6,7), and we need to find the point A' which is the reflection of point A across the x-axis.
the point A is represented in the following image:
And the reflection across the x-axis is like if we reflected the point in a mirror:
As we can see the point A' has the coordinates:
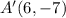
As a general rule, when we make a reflection of a point
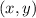
the reflection across the x-axis gives the point:
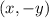
We change the sign of the y-coordinate.
Like in this case (6,7) became (6,-7).
Answer: (6,-7)