Question

A metal wire has a resistance of 10.0 Ω at a temperature of 20oC. At 90oC, its resistance increases to 10.5 Ω. What is the temperature coefficient of resistivity of this metal?Group of answer choices1.27x10-4 oC-11.27x10-5 oC-17.24x10-4 oC-17.24x10-5 oC-1

Answer 1

Take into account that the resistance in the wire, for a certain temperature T, can be written as follow:

`R=R_o(1+\alpha T)`

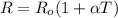
where,

Ro: initial resistance

T: temperature

α: coefficient of resistivity

R: resistance

Based on the given information, you can write for each temperature:

`\begin{gathered} 10.0\Omega=R_o(1+\alpha\cdot20C) \\ 10.5\Omega=R_o(1+\alpha\cdot90C) \end{gathered}`

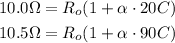
If you divide the first equation over the second one, you have:

`(10.0\Omega)/(10.5\Omega)=(R_o(1+\alpha\cdot20C))/(R_o(1+\alpha\cdot90C))`

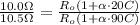
By solving for α, you obtain:

`\begin{gathered} 10.0\Omega(1+\alpha\cdot90C)=10.5\Omega(1+\alpha\cdot20C) \\ 10.0+\alpha\cdot900C=10.5+\alpha\cdot210C \\ \alpha(900C-210C)=10.5-10.0 \\ \alpha(690C)=0.5 \\ \alpha=(0.5)/(690C)=7.24\cdot10^(-4)C^(-1) \end{gathered}`

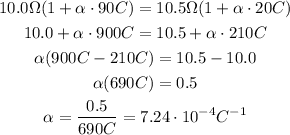
Hence, the coefficient of the resistivity of the given metal is approximately

7.24*10^-4°C^-1