Take into account that the resistance in the wire, for a certain temperature T, can be written as follow:
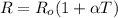
where,
Ro: initial resistance
T: temperature
α: coefficient of resistivity
R: resistance
Based on the given information, you can write for each temperature:
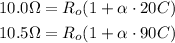
If you divide the first equation over the second one, you have:
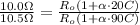
By solving for α, you obtain:
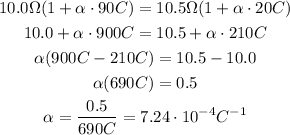
Hence, the coefficient of the resistivity of the given metal is approximately
7.24*10^-4°C^-1