We have a system of equations:
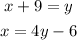
We can solve it by substitution, using the equality of the first equation, replacing y in the second equation:
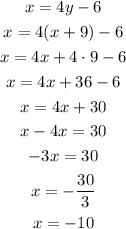
With the value of x, we can calculate y as:
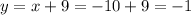
The solution expressed as ordered pair is (x,y) = (-10,-1).
Answer: (-10, -1)