Notice that the figure on the picture is an isosceles trapezoid, then, the base angles are equal and we would have the following expression:
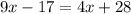
solving for x, we get:
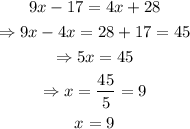
now that we know the value of x, we can find the explicit value of angle Q:
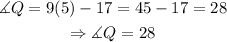
next, we know as a general rule that the angles in a trapezoid that are adjacent are supplementary, then, we have the following:
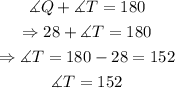
therefore, the measure of angle T is 152 degrees