Given
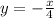
We know that the general equation for a circle is given by:

Since the circle for this case is centered at the origin then h,k =0 and we have this:
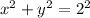
For this case we can replace the formula for y from the line into equation (1) and we got:

Divide both sides by 17

Now we just need to replace into the original equation for the line and we get the y coordinates like this:
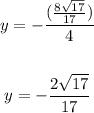
and
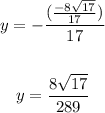
The final answer
