Question

During the investigation of a traffic accident, police find skid marks 55 meters long. They determine the coefficient of kinetic friction between the car's tires and the roadway to be 0.486 for the prevailing conditions. How fast was the car going when its brakes were applied?

Answer 1

Assuming that the force of friction was the only force on the horizontal plane we have, using Newton's second law, that:

`-F_f=ma`

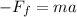
The minus sign indicates that the force is going againts the motion.

Now, the force of friction is given by:

`F_f=\mu N`

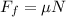
where mu is the coeffient of friction and N is the normal force. In this case the normal force is equal to the weight of the car, then our equation of motion is:

`\begin{gathered} \\ -\mu mg=ma \end{gathered}`

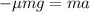
Solving for a we have that:

`\begin{gathered} a=-\mu g \\ a=-(0.486)(9.8) \\ a=-4.7628 \end{gathered}`

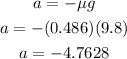
Therefore the acceleration is -4.7628 meters per second per second.

Now that we know the acceleration we can use the formula:

`v^2_f-v^2_0=2a(x-x_0)_{}`

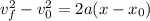
To find how fast the car was going. In this case the final velocity is zero and the change in position is 55 meters, plugging the values we have that:

`\begin{gathered} 0^2-v^2_0=2(-4.7628)(55) \\ v^2_0=523.908 \\ v_0=\sqrt[]{523.908} \\ v_0=22.9 \end{gathered}`

Therefore the initial velocity of the car was 22.9 meters per second.