Given:
rate (r) = 2% or 0.02 in decimal form
compounding period (m) = quarterly = 4 times every year
Regular payment every quarter (R) = $1364
time (t) = 3 years
Find: Future Value
Solution:
The formula for future value of an ordinary annuity is:
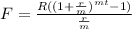
These variables in the formula have already there values given in the problem. We have listed them above as well.
Let's plug in those given data to the formula to solve for F.
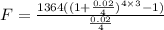
Simplify.
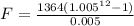

Answer: At the end of 3 years, Chang's annuity will have become $16, 825.71.