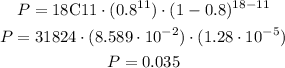Question

Find the probability of X successes, using Table B in Appendix A of the textbook or some other method.n = 18, p = 0.8, X = 11

Answer 1

This kind of exercise refers to the probability of exatly "x" successes on "n" repeated trials in an experiment which has a possible outcome.

If the probability of succes on an individial trial is p, then the probability is represented by:

`P=\text{nCx}\cdot p^x\cdot(1-p)^(n-x)`

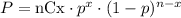
Here nCx indicates the number of different combinations of x objects selected from a set of n objects.

Using the given data, we have:

`\begin{gathered} P=18\text{C11}\cdot(0.8^(11))\cdot(1-0.8)^(18-11) \\ P=31824\cdot(8.589\cdot10^(-2))\cdot(1.28\cdot10^(-5))^{} \\ P=0.035 \end{gathered}`