Given that twenty pairs of measurements were taken at random to estimate the relation between variables X and Y, you need to remember that, by definition:
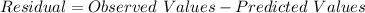
You can identify that the residual plot has a pattern that looks like a parabola.
By definition, when the pattern of a residual plot has a clear pattern, then a line is not an appropriate model to fit the relation between the variables.
Therefore, in this case, the model is a non-linear model.
Hence, the answer is: Option B.