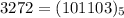Question

Convert 3278 to a numeral in base 5

Answer 1

To convert a number in base 10 to a number in base five we need to divide the number by 5 and find its reminder for the firt step we would have:

`(3278)/(5)=655.6`

since we have a decimal part this means that it has a remainder, to find it we mutiply the integer part of the previus result to five and subtract the result from 3278, then we have:

`3278-(5)(655)=3`

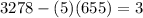
This means that our first remainder is 3.

Now we need to divide the previous interger result (655) by 5 and then find the remainder as we did before:

`(655)/(5)=131`

Since this result does not have decimal part the remainder is zero.

This means that our second remainder is 0.

We apply the same procedure till we have a quotient in which the result is less than 5, then we will have:

`\begin{gathered} (131)/(5)=26.2\text{ Integer result 26, remainder 1} \\ (26)/(5)=5\text{ Integer result 5, remainder 1} \\ (5)/(5)=1\text{ Interger result 1, remainder 0} \\ (1)/(5)=0\text{ Integer result 0, remainder 1} \end{gathered}`

This means that our remainders are 3, 0, 1, 1, 0, 1.

The number in base 5 is the number formed bu the remainders in the opposite order, therefore:

`3272=(101103)_5`