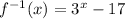Question

PLEASE EXPLAIN IN DETAIL PLS SO I CAN UNDERSTAND BETTER

Answer 1

Find the inverse function of:

`f(x)=\log_3(x+17)`

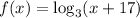
First, call the function y = f(x):

`y=\log_3(x+17)`

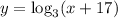
We have to solve for x. We need to apply the definition of logarithms:

If:

`\begin{gathered} a=b^x \\ \text{ Then:} \\ \log_ba=x \end{gathered}`

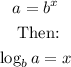
It can be applied in inverse order, that is, if:

`\begin{gathered} x=\log_ba \\ \\ \text{ Then:} \\ \\ a=b^x \end{gathered}`

Applying the definition above:

`x+17=3^y`

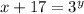
Subtract 17:

`x=3^y-17`

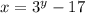
Now we change x for y and vice-versa:

`y=3^x-17`

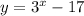
Finally, substitute y for the inverse of f(x):

`f^(-1)(x)=3^x-17`