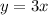Solution:
Given that y varies directly as x, this implies that
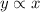
Introducing a constant of variation K, we have
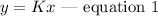
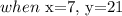
Thus, by substituting these values into equation 1, we have
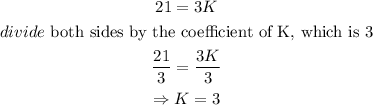
The constant of variation is
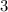
By substituting the value of K into equation 1,
we have the equation of the direct variation to be