The slope-intercept form of the line has the following form below:

In the question, the data given are:
slope = -3
point = (-4, 10)
y - coordinate = 10
x - coordinate = -4
To be able to solve the equation of the line given slope and a point, we can use the following formula below:

where:
m = slope
y₁ = y - coordinate of the point that goes through the line
x₁ = x - coordinate of the point that goes through the line
Let's substitute the given data with the formula we have.
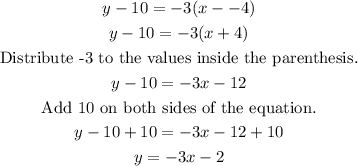
Therefore, the equation of this line in slope-intercept form is:
y = -3x - 2.