Question

[Use g = 10 m/s2, use the values of sine, cosine, and tangent found on the AP Physics Table of Information.]An artillery shell is fired with an initial velocity of 500 m/s at an angle of 53° from the level ground.(a) How much time passes before the shell strikes the ground? _________s(b) What horizontal distance does the shell travel before striking the ground?_________m

Answer 1

Part (a)

The time taken by the shell to strike on the ground can be given as,

`t=(2u\sin \theta)/(g)`

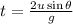
Plug in the known values,

`\begin{gathered} t=\frac{2(500\text{ m/s)sin53}}{10m/s^2} \\ =(100\text{ s)(}0.799) \\ \approx80\text{ s} \end{gathered}`

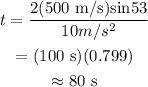
Therefore, the time after which the shell strikes on the ground is 80 s.

Part (b)

The horizontal distance covered by the shell is,

`d=u_xt`

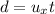
The horizontal speed of the shell is,

`u_x=u\cos \theta`

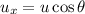
Therefore, the distance covered becomes,

`d=(u\cos \theta)t`

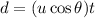
Substituting values,

`\begin{gathered} d=(500\text{ m/s)cos53(80 s)} \\ =(40000\text{ m)(}0.602) \\ =24080\text{ m} \end{gathered}`

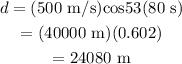
Therefore, the horizontal distance covered by the shell is 24080 m.