$67247.39
Step-by-step explanation
Step 1
find the average of the 3 highest years salaries
Let
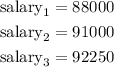
hence

Step 2
find the 2.125 % of salary average
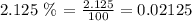
so, to find the 2.125 % of any number, multiply the number by 0.02125
Hence
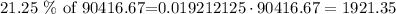
Step 3
find the pension
pension that is calculated by multiplying the number of years worked times 2.125% of the average of the 3 highest year's salaries.
Let
years John worked=35
replace
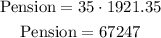
I hope this helps you