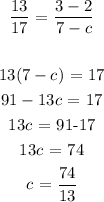Question

Find c such that (7, 3), (-10, -10) and (c, 2) lie on a line. C = _________

Answer 1

Step-by-step explanation:

Here, we want to get the value of c given that the three points are collinear

When points are collinear, the slope between any two is same

Two or more points are called collinear if they lie on the same line

Mathematically, we have the expression of calculating the slope as:

`m\text{ = }(y_2-y_1)/(x_2-x_1)`

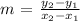
For the first 2, we have:

`m\text{ = }(-10-3)/(-10-7)\text{ = }(13)/(17)`

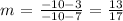
Now, to get the vale of c, we can use any of the points:

`\begin{gathered} (13)/(17)\text{ = }(3-2)/(7-c) \\ \\ 13(7-c)\text{ = 17} \\ 91-13c\text{ = 17} \\ 13c\text{ = 91-17} \\ 13c\text{ = 74} \\ c\text{ = }(74)/(13) \end{gathered}`