The points we have are:
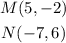
We label this points as follows for reference:
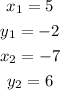
We have that the ratio is:
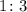
Where we will call a=1 and b=3.
And we use the following formula for finding the coordinates of a point given the two endpoints and the ratio:
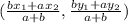
Substituting our values:
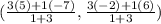
We solve the operations:
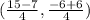
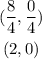
Point P is at (2,0)