Question

Write an equation of the parabola in intercept form. (3, 4) (4, 0) (2, 0) An equation of the parabola is y=

Answer 1

Question:

Solution:

The intercept form of a quadratic equation (a parabola) is given by the following formula:

`y\text{ = }a(x-p)(x-q)`

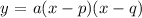
where p and q are the x-coordinate of the x-intercept of the parabola. In this case, notice that:

p = 2 and q = 4

then we have the preliminary equation:

EQUATION 1:

`y\text{ = }a(x-2)(x-4)`

now, to find a, replace the point (x,y) = (3,4) in the previous equation. so that, we obtain:

`4\text{ = }a(3-2)(3-4)`

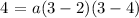
this is equivalent to:

`4\text{ = }a(1)(-1)\text{ = -a}`

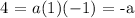
thus

`a\text{ = -4}`

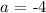
then, replacing a = -4 into the EQUATION 1, we get:

`y\text{ = -4}(x-2)(x-4)`

Then, we can conclude that the equation of the given parabola in the intercept form is:

`y\text{ = -4}(x-2)(x-4)`