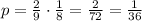Question

There are 7 apples and 2 oranges in a bag. Determine each probability:e.Selecting 2 apples with replacement:Independent or dependent?Probability?f. Selecting 2 apples without replacement:Independent or dependent?Probabilitv?

Answer 1

e.

Independent

Probability = 4/81

f.

Dependent

Probability = 1/36

Explanation:

The first thing is to define the dependent and independent events:

Two events are independent if the outcome of the second event is not affected by the outcome of the first event and both events are dependent if the outcome of the first event affects the outcome of the second event so the probability is changed.

e.

In this case the event is independent, since the apples to be replaced, the probability does not change.

The probability in this case would be the number of apples divided by the total number of fruits in the bag, in the first event and in the second event it would be the same probability, the final probability would be the product, thus:

`p=(2)/(9)\cdot(2)/(9)=(4)/(81)`

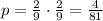
f.

In this case the event is dependent, since the apples are not replaced, the probability changes.

The probability in this case would be the number of apples divided by the total number of fruits in the bag, in the first event and in the second event it would be taking into account that there is 1 less apple and one less fruit in total, the final probability would be the product, therefore:

`p=(2)/(9)\cdot(1)/(8)=(2)/(72)=(1)/(36)`