1 Answer

We · Answer 1 · 2023-03-12T07:08:47+0000

Answer:

y = -1 (x - 6)

Explanations:

The point - slope form of the equation of a line is:

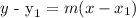
$y\text{ - y}_1=m(x-x_1)$

Where m represents the slope, and can be calculated using the equation:

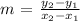
$m\text{ = }(y_2-y_1)/(x_2-x_1)$

The line passes through the point (6, 0) and (0, 6)

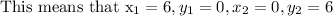
$\text{This means that x}_1=6,y_1=0,x_2=0,y_2=6$

Calculating the slope using the formula given above:

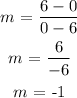
$\begin{gathered} m\text{ = }(6-0)/(0-6) \\ m\text{ = }(6)/(-6) \\ m\text{ = -1} \end{gathered}$

Substituting the values of m, x1, and y1 into the point slope form of the equation of a line:

y - 0 = -1 (x - 6)

y = -1 (x - 6)

Please log in or register to add a comment.